LLM高速化へ新手法Dynasorで効率と精度向上

言語・LLM
  • LLM推論効率化のためにCertainties概念を導入
  • Certaintiesに基づくリソース配分手法Dynasorを提案
  • Dynasorは計算効率と応答精度の向上を実現

論文：Efficiently Serving LLM Reasoning Programs with Certaindex

本記事で使用している画像は論文中の図表、またはそれを参考に作成した画像を使用しております。

本論文の概要

この論文では、LLM（大規模言語モデル）の推論プログラムを効率的に提供するための「Certainties」という新しい概念を紹介し、これを活用したリソースの割り当て手法「Dynasor」を提案しています。

Dynasorシステムの設計を示しています。このシステムは、推論プログラムの進捗を測る指標「Certaindex」を活用して、計算リソースを最適に割り当てる仕組みを持っています。図の(a)では、Dynasorの全体的なアーキテクチャが示されており、「推論プログラムの抽象化」、「アプリケーション実行環境」、「システム実行環境」の3つの主要コンポーネントで構成されています。図の(b)では、推論プログラムのインターフェースが示されており、Certaindexを更新する関数と、推論アルゴリズムを実行する関数の実装が開発者に求められます。図の(c)では、Self-Consistencyプログラムの簡単な実装例が示されており、Certaindexを用いて計算リソースの割り当てを調整しながら推論を進めていく仕組みが解説されています。

LLMは、多様なタスクを迅速に解決する能力がありますが、その計算需要が非常に高いため、推論の効率化が求められています。この論文では、特に複雑な推論アルゴリズムのためのリソース配分を最適化する方法を提案しています。Certaintiesを導入することで、より効果的なリソース管理を実現し、応答時間と精度を向上させることを目的としています。

Certaintiesの概念

この論文は、推論プロセスの中で段階的に達成される「確信度」（Certainties）を定量的に評価し、それを考慮に入れたリソースの動的割り当てを行うことを提案しています。

さまざまなLLM推論アルゴリズムの概要を示しています。Self-Consistency（SC）アルゴリズムでは、複数の独立した推論経路を生成し、それぞれが異なる解答を出します。最終的には、多数決によって最も頻繁に現れる答えを選択します。Rebaseアルゴリズムでは、推論の中間ステップを生成し、それらを報酬モデルで評価して、スコアの高いものを次のステップでさらに展開します。Monte Carlo Tree Search（MCTS）アルゴリズムは、解をツリーのノードとして表現し、ノードを順次展開、スコア付けし、その結果を木構造に反映させながら最終解を導き出します。内部化されたChain-of-Thought（ICoT）は、モデルが一連の推論を生成し、過去の出力を考慮しながら解答を改良するプロセスを繰り返します。これらすべてのアルゴリズムにおいて、計算量を調整するためのコントロールパラメータ（例：SCでは生成経路数、MCTSでは探索イテレーション数）が重要な役割を果たします。

具体的には、モデルの推論が進むにつれて、答えが正しいと確信できる度合いを計測し、それに基づいて必要な計算リソースを調整します。これにより、無駄な計算を省き、より効率的な推論が可能になります。

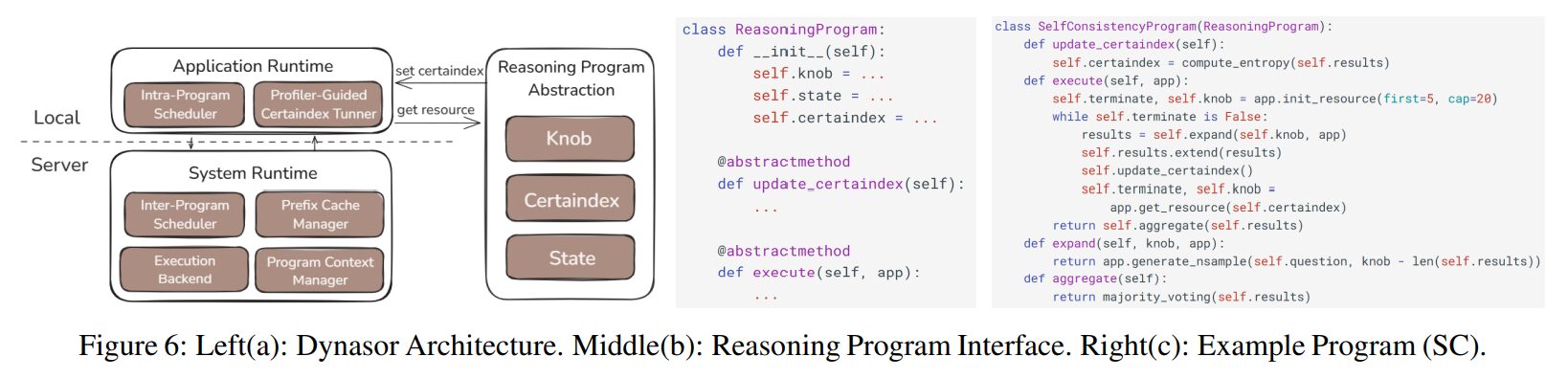
提案手法：Dynasor

  1. Certaintiesの測定: 筆者たちは、さまざまな推論ステップでCertaintiesを測定するメカニズムを開発しました。これは、各ステップで生成された結果がどれだけ正確であるかを示します。

  2. スケジューリング戦略: Certaintiesの値に基づいて、Dynasorは推論プログラムに対するリソースの割り当てを自動的に調整します。特に、より高い確信度が得られた場合には、計算リソースを他のタスクに割り当て、全体の効率を向上させます。

実装方法は以下の通り。

  • プログラム間のスケジューリング: 異なるプログラムに対して動的にリソースを配分します。これにより、複数のタスクを効率的に並行処理できます。

  • ガングタイミングの調整: 並列に実行されるタスクの終了時間を同期するための戦略を採用し、システム全体のスループットを最大化します。

実験結果

この論文では、提出された手法をベースにした実験が行われ、以下のような成果が示されています。

  1. 計算効率の改善: Certaintiesを利用した推論では、標準的な手法と比較して最大30%のリソース節約が可能であるとされています。

  2. 応答精度の向上: Certaintiesベースの手法は、正解率を維持しつつ、より少ないステップ数で重要な情報に到達できることが示されました。

  3. 柔軟な運用の実現: Dynasorを利用することで、様々なプラットフォーム間での柔軟なリソース調整が可能となり、実用的な運用が可能です。

この研究により、LLMの推論を効率化するための新たなアプローチが提案され、今後のLLM運用のコスト削減や効率化に貢献する可能性が示されました。今後の研究では、さらなるスケーラブルな展開やリアルタイムでの適応性向上が求められています。

図表の解説

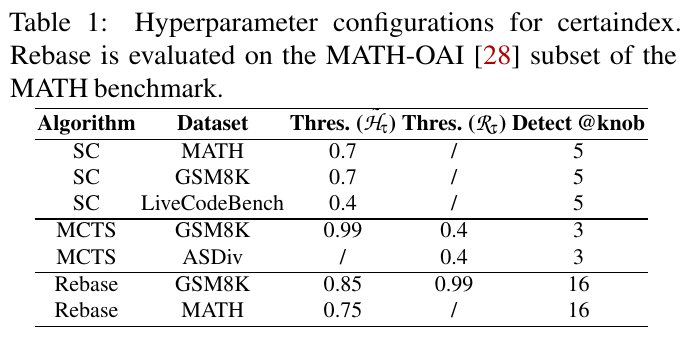
この表は、さまざまなアルゴリズムとデータセットにおけるハイパーパラメータの設定を示しています。具体的には、セルタインデックスという手法が MATH-OAI のサブセットで評価されています。

  • アルゴリズム（Algorithm）: SC（Self-Consistency）、MCTS（Monte Carlo Tree Search）、Rebase が使用されています。
  • データセット（Dataset）: MATH、GSM8K、LiveCodeBench、ASDiv が示されています。
  • しきい値（ しきい値は、アルゴリズムによって異なり、決定規則に使われる数値です。
  • 検出ステップ（Detect @knob）: 各アルゴリズムでの詳細な設定や検出ステップを示します。
  • これらの設定は、推論時の計算資源の割り当てを最適化し、性能を向上することを目的としています。

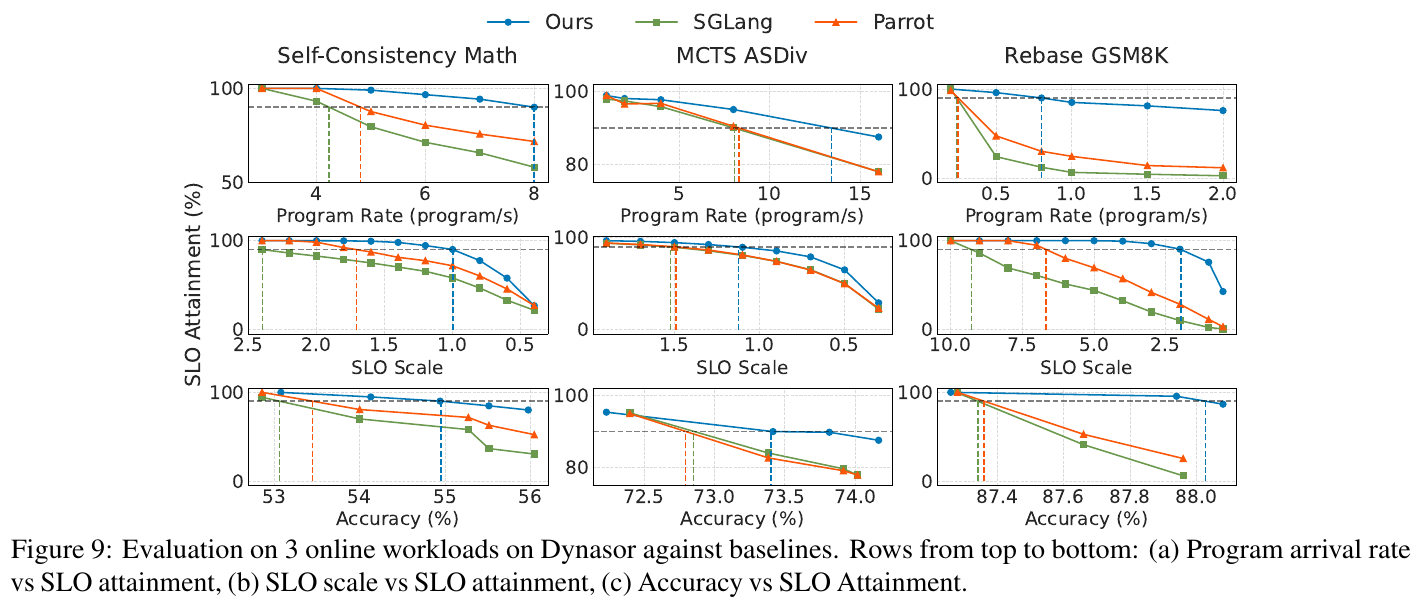
この図表は、Dynasorシステムの評価結果を示しています。Dynasorは、大規模言語モデル（LLM）の推論時におけるコンピュートリソースの効果的な配分を目的としたシステムです。図は3つのワークロード（Self-Consistency Math、MCTS ASDiv、Rebase GSM8K）において、異なる条件でのSLO（サービスレベル達成率）を示しています。

  • 上段の行では、プログラム到着率（プログラム/秒）とSLO達成率の関係が示されています。Dynasorは、他のベースラインと比較して、より高いリクエスト処理率を達成しています。
  • 中段は、SLOスケールとSLO達成率の関係を示し、Dynasorがより厳しいSLOを保持できることを示しています。
  • 下段は、精度とSLO達成率の関係を示しており、Dynasorは同じSLO達成率を維持しながら高い精度を実現しています。 これにより、Dynasorは、精度を保ちながらリソースの効率的な配分が可能であることが示されます。

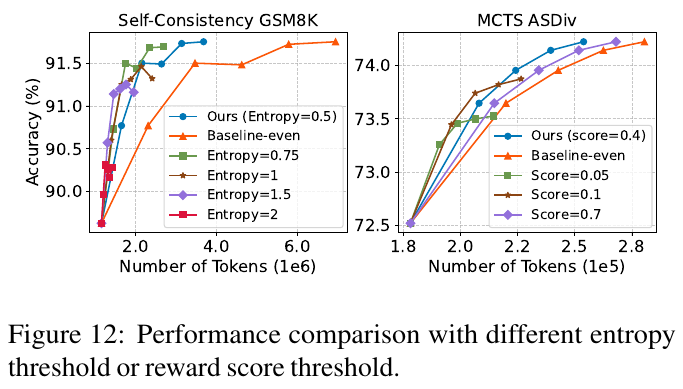
図12は、異なるエントロピーや報酬スコアの閾値による性能比較を示しています。左のグラフでは、自己一致性アルゴリズムを用いた場合のGSM8Kデータセット上で、トークン数の増加に伴う精度の上昇を示しています。様々なエントロピーパラメータを持つアルゴリズムの性能を比較しており、高いエントロピーでは精度が若干低下する傾向が見られます。右のグラフはMCTSアルゴリズムのASDivデータセットにおける性能を示しており、スコアが変わると精度がどう変動するかを示しています。高いスコア閾値だと精度は向上するものの、コスト増が生じ得ることがわかります。これらの結果は、アルゴリズムのチューニングにおいて、パラメータ選択が重要であることを示唆しています。

この図表は、ある論文の一部で、オンライン作業負荷の設定を示しています。具体的には、3つのアルゴリズム（SC、MCTS、Rebase）が示されています。それぞれのアルゴリズムが使用するデータセット、LLM（大規模言語モデル）、報酬モデル、基本的な期限（秒単位）が記載されています。 – SCはMATHデータセットに対してLlama3.1 8Bモデルを使用し、報酬モデルはなし、期限は240秒です。 – MCTSはASDivデータセットに対してLlama2 7Bモデルを用いており、報酬モデルはSkywork 7Bで、期限は60秒です。 – RebaseはGSM8Kデータセットに対してLlemma 34Bモデルと報酬モデルを用いており、期限は300秒です。 この設定は、これらのアルゴリズムがどのように異なる条件で動作するかを比較するために用いられます。

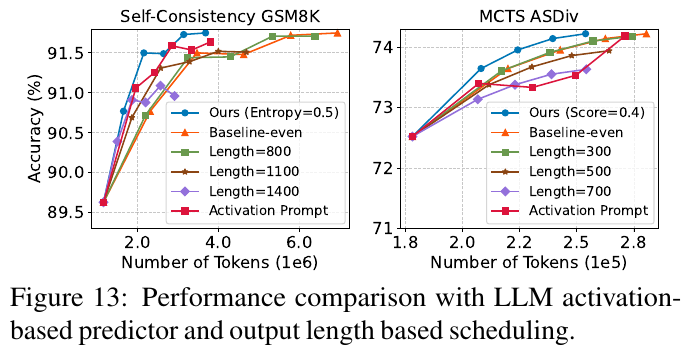
図13は、LLM（大規模言語モデル）の推論アルゴリズムに対するトークン数と精度の関係を示しています。左のグラフは、GSM8Kデータセットでの自己整合性アルゴリズムのパフォーマンスを、右のグラフはASDivデータセットにおけるMCTSアルゴリズムのパフォーマンスを示しています。横軸はトークン数、縦軸は精度を表しています。 どちらのグラフも、より多くのトークン数が使用されるとモデルの精度が向上し、その後プラトーに達することを示しています。

さらに、異なるアルゴリズムや設定（例：エントロピーやスコアの閾値、固定長）に基づいた比較も行われています。結果として、Dynasorというシステムを用いることで、計算コストを抑えつつ精度向上が見込めることが示されています。この手法は、特に難易度に応じて計算を調整することで、リソースの効率的な利用と精度のバランスを取ることを目的としています。

タイトルとURLをコピーしました