- 複雑な推論能力を向上させるフレームワーク「Meta-CoT」を提案
- モデルの正確性と自己修正能力を高める手法として自己強化型学習法やバックトラッキング機能を導入
- 高難度の数学的タスクで優れた性能を示し、特別に設計されたデータセット「Big MATH」が訓練に貢献
論文:Towards System 2 Reasoning in LLMs: Learning How to Think With Meta Chain-of-Though
本記事で使用している画像は論文中の図表、またはそれを参考に作成した画像を使用しております。
本論文の概要
この論文では、大規模言語モデル(LLM)が複雑な推論能力を向上させるための新たなフレームワークである「Meta Chain-of-Thought(Meta-CoT)」を提案しています。この手法は、従来の推論プロセスの欠点を克服するため、推論の各ステップを明確にし、その過程を「メタレベル」でモデル化することで、モデルの正確性や自己修正能力を高めることを目的としています。
Meta-CoTは、主に数学的問題や定理証明のような段階的推論が必要なタスクで使用され、その手法をいくつかの側面で展開しています。具体的には、まず自己強化型の学習法である「Self-Taught Reasoner (STaR)」を活用して、モデルがステップごとの推論をより正確に学習できるようにします。また、Meta-CoTは計算効率を考慮しつつ、探索アルゴリズムを統合し、計算過程を動的に検証するバックトラッキング機能を導入しました。これにより、モデルが中間ステップの誤りを自動的に認識し、それを修正する能力が強化されます。
実験結果として、Meta-CoTを適用したモデルは、特に難易度が高い数学的タスクで顕著な性能向上を示しました。これには、独自に設計した学習データセット「Big MATH」が重要な役割を果たしています。このデータセットは、推論プロセスを正確に反映した問題解を多く含むため、Meta-CoTモデルの訓練に適しています。
さらに、この論文では、強化学習(RL)を取り入れた後処理手法を提案し、これがモデルの性能をさらに向上させることを確認しています。また、Meta-CoTの有効性を検証するために、Monte Carlo Tree Search(MCTS)などの探索アルゴリズムを用いることで、モデルがより複雑な問題を解く能力を示しました。
図表の解説
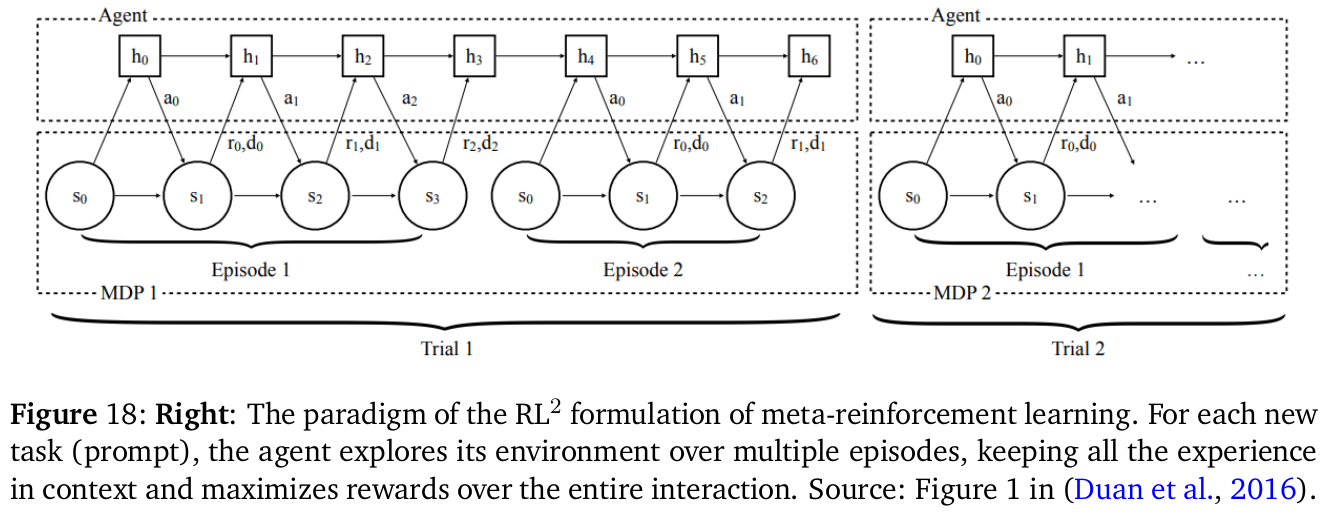
この図は、メタ強化学習のRL²形式を示しています。それぞれの新しいタスク(プロンプト)に対して、エージェントは環境を複数のエピソードを通じて探索します。この間、エージェントはコンテキスト内の経験をすべて保持し、全体の相互作用を通じて報酬を最大化します。各トライアルは、異なるマルコフ決定過程(MDP)として構成され、エピソードを通して状態と行動が変化し、それにより報酬が得られます。この図は、RL²がどのようにしてタスクの学習と適応を進めるかの過程を簡略化して示しています。
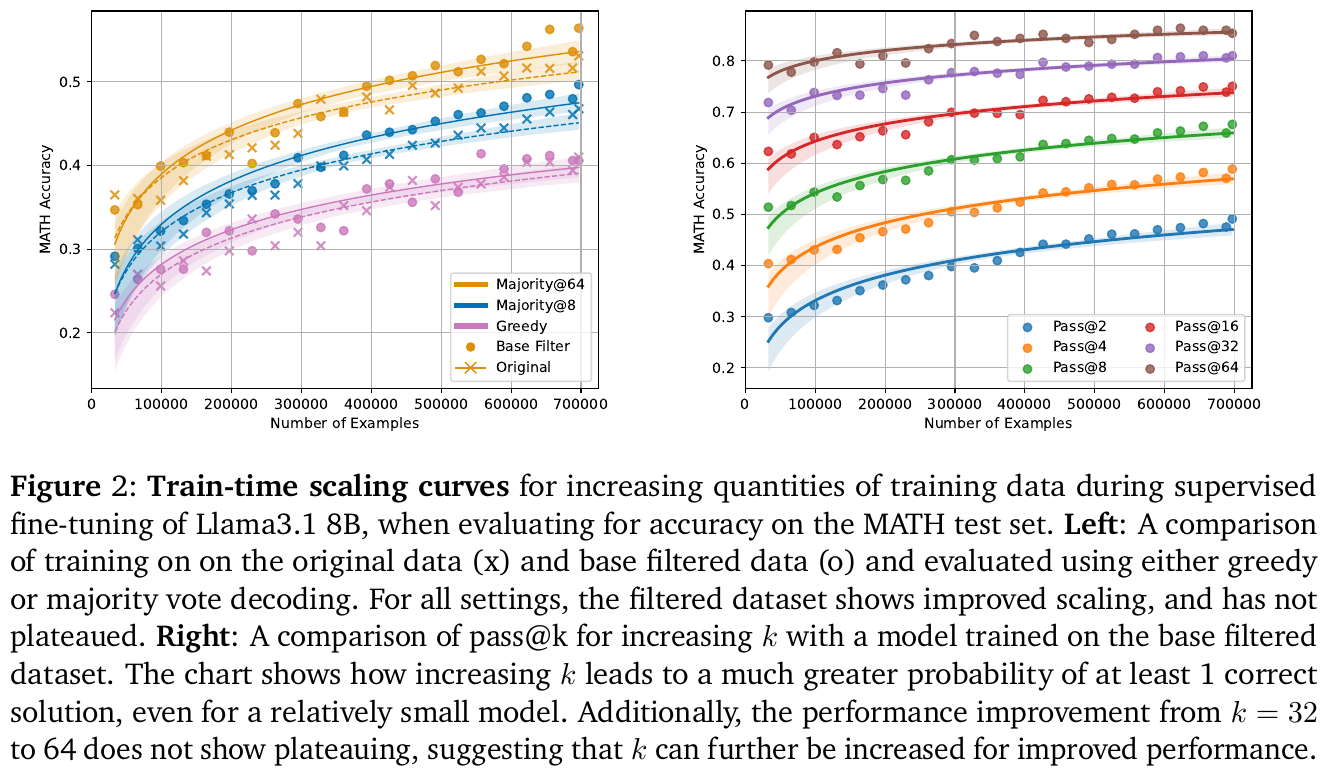
画像の図2は、大規模言語モデルの学習におけるデータ増加の効果を示しています。 左側のグラフは、元のデータとフィルタリングされたデータに基づく学習結果を比較し、元のデータ(×)とフィルタリングされたデータ(o)の両方でスケーリングが改善されることを示しています。フィルタリングされたデータセットは、グリーディーデコーディングおよび多数決デコーディングのどちらでもプラトーしていません。 右側のグラフは、異なるk値におけるpass@kの比較を示し、kの増加が少量のモデルでも1つ以上の正解を得る確率を大幅に増大させることを示しています。特に、k=32から64への改善がプラトーせず、さらなる性能向上のためにkを増やす余地があることを示唆しています。
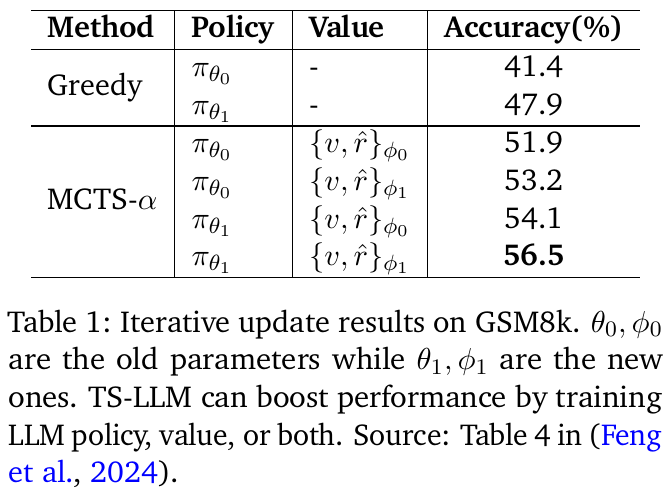
この表は、GSM8kデータセットに対する逐次更新の結果を示しています。古いパラメータを持つポリシー($\pi_{\theta_0}$)と新しいパラメータを持つポリシー($\pi_{\theta_1}$)の性能を比較しています。Greedy法では、最初のパラメータセットでは41.4%、更新後は47.9%の精度を達成しました。MCTS-α法ではさらに高い精度が得られ、最大で56.5%に達しています。これはポリシーや価値関数の改善によって精度が上がったことを示唆しています。この結果、TS-LLMがLLMのポリシーや価値関数を学習させることで性能向上につながる可能性を示しています。

この画像は、論文内でアルゴリズム的推論、初等学校の数学(GSM8k)、そしてGSM8kからMATHへの転送における検証モデルのスケーリングトレンドを示しています。画像内の各グラフは、異なる「ベスト・オブ・N」スケーリング設定(Nが増加する場合)の下で、問題解決の効率性を視覚化しています。各右上に示されている倍率(例えば「1.5x efficient」)は、特定の条件下での効率化を表しています。これにより、解の数に応じて検証モデルの精度が向上することが示されています。Nが増えるにつれて、どのモデルもより良い解を提供できるようになります。
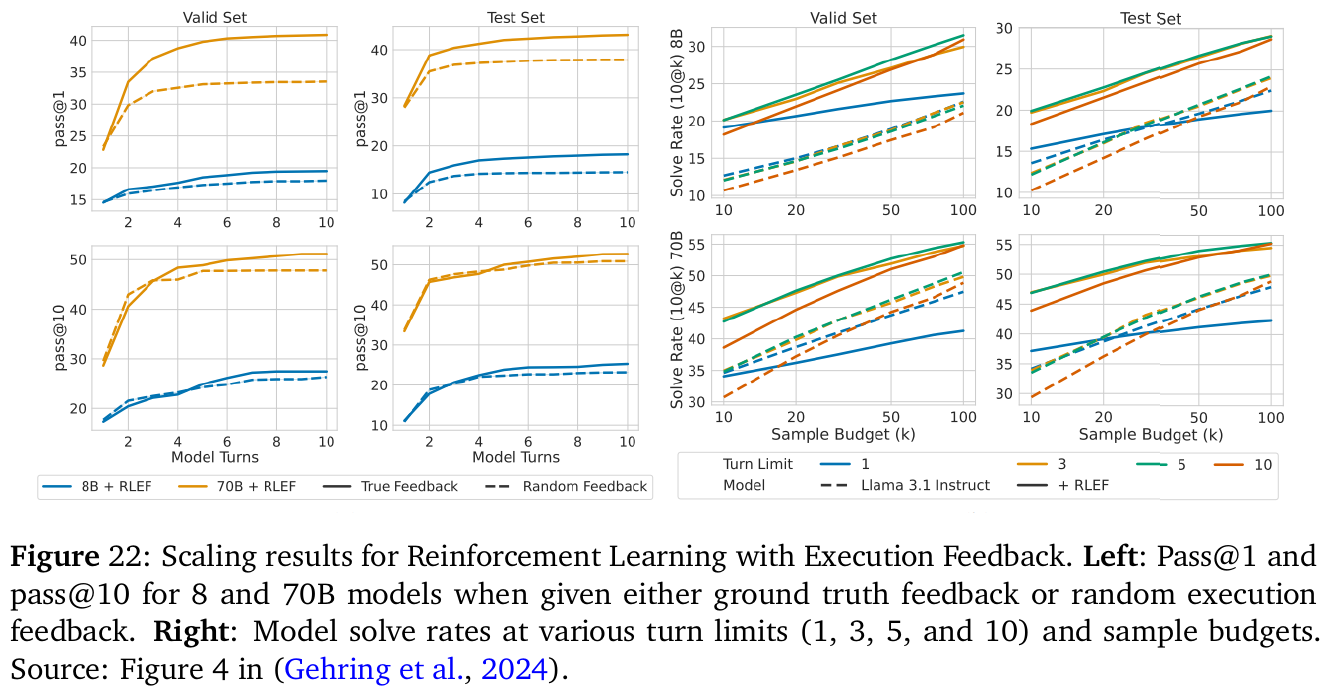
この図は、強化学習(Reinforcement Learning)を通じてモデルがどのようにスケーリングしているかを示しています。左側のグラフでは、異なるターン回数(1回から10回まで)に対する8Bと70Bモデルの性能をテストデータと検証データセットで示しています。モデルが「パス」した割合(正確な解を出した割合)が増加する様子が示されています。特に、ターン数が増えるとモデルの精度が向上することがわかります。右側のグラフでは、さまざまなサンプル予算の下でのモデルの問題解決率をプロットしており、サンプル数が増えると解決率も向上することが示されています。これらの結果は、モデルが多くの計算資源を利用することでより良い解を見つけられることを示しています。
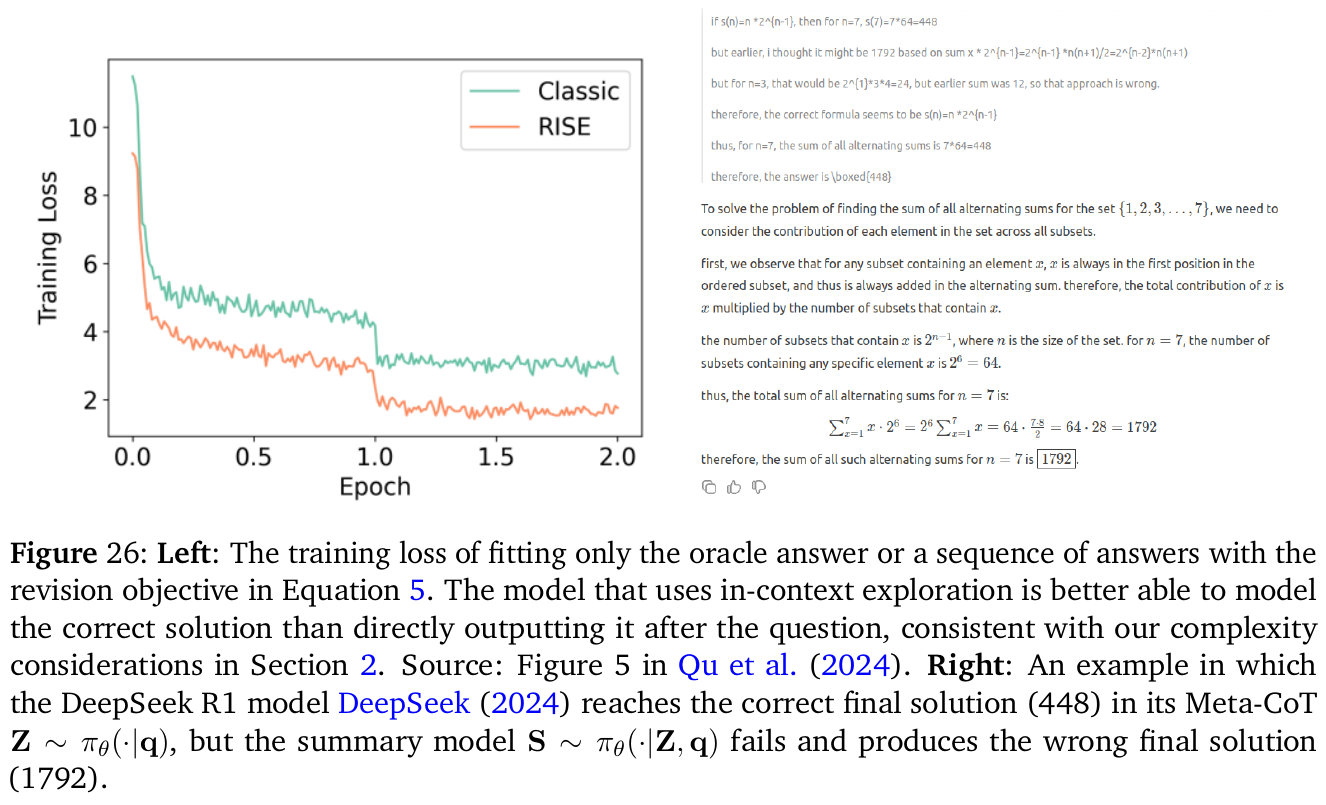
この画像は、論文の一部を示しており、特に2つの異なるトレーニングモデル「Classic」と「RISE」のトレーニング損失のグラフです。このグラフは、横軸にトレーニングのエポック数を、縦軸にトレーニング損失を示しています。 評価されているのは、トレーニング中にモデルが損失をどのように減少させていくかという点です。一般に、損失が減少することでモデルの精度が向上することを意味します。「RISE」モデルの方が損失が小さくなる傾向が見られ、より効果的に学習できていることを示唆しています。 右側の数式は、与えられた問題の解を求めるための数学的過程を説明しています。この数式と文章は、特定の数学操作によって解が求められることを示しています。
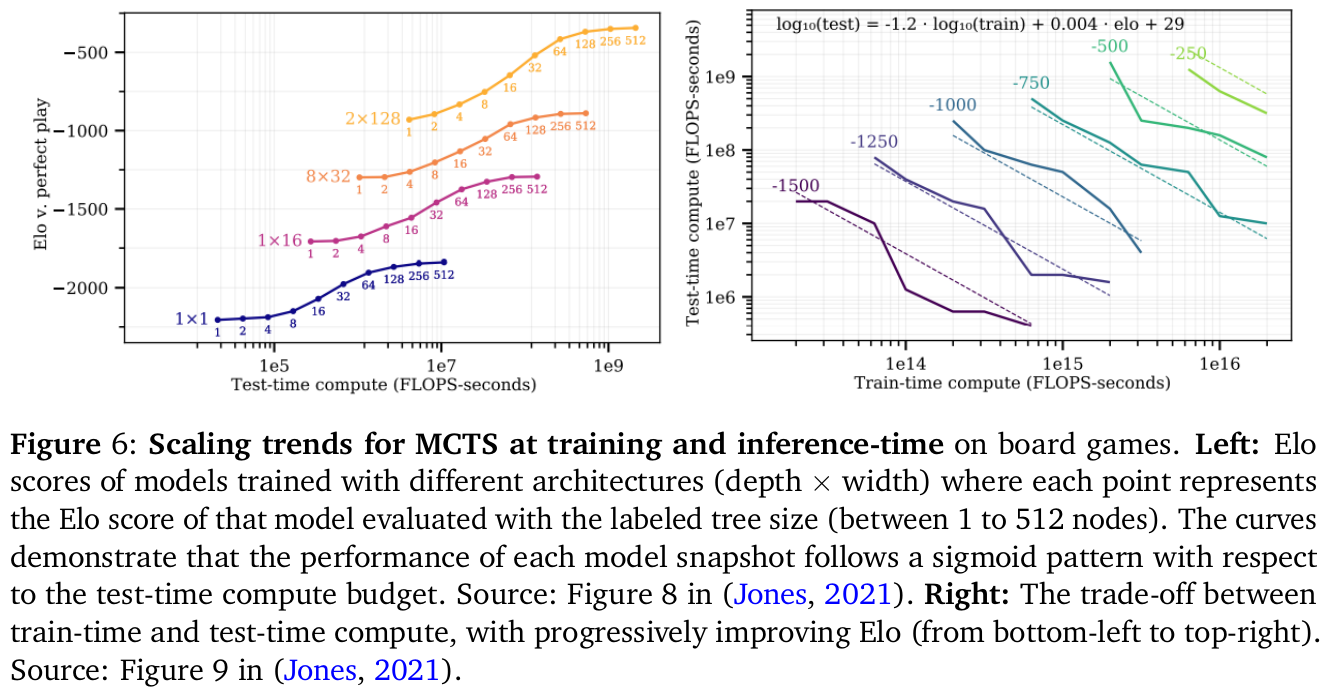
この図は、ゲームにおけるモンテカルロ木探索(MCTS)の学習と推論のスケーリング傾向を示しています。左側の図は、異なるアーキテクチャのモデルのEloスコアを表しており、それぞれのポイントはモデルの木のサイズに基づいたEloスコアを示しています。曲線は、テスト時の計算量に対する各モデルの性能がシグモイドパターンに従うことを示しています。右側の図は、トレーニングとテスト時 compute のトレードオフを示しており、Eloが進行的に向上しています。これによって、モデルが増加する計算リソースとともに強化されることが示されています。
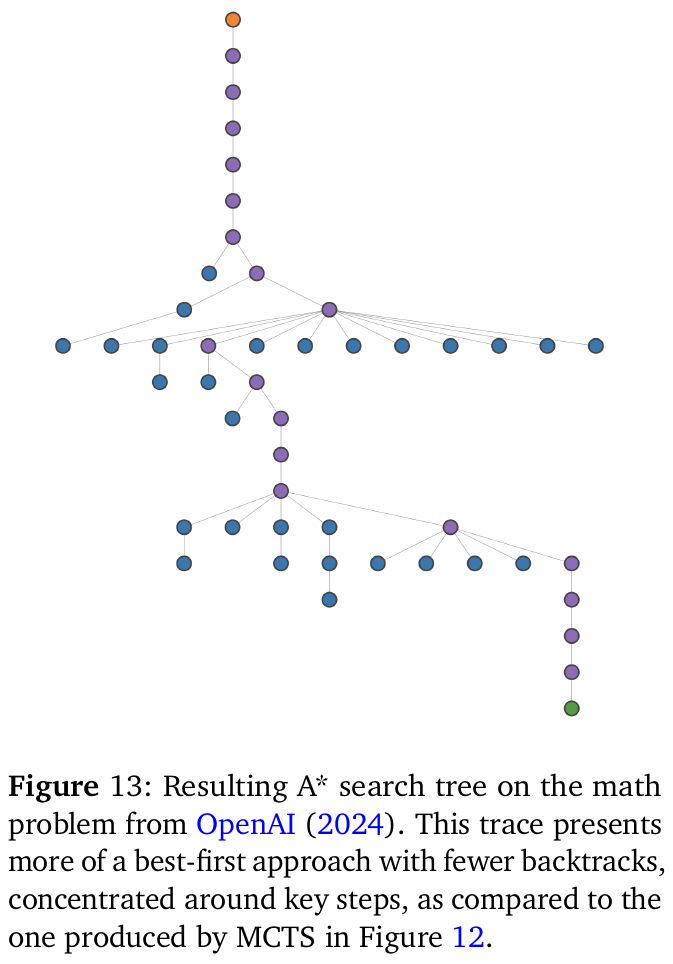
図13は、数学問題におけるA*探索木を示しています。この図は、OpenAI (2024) による実験結果です。A*アルゴリズムは、探索空間を効率的にナビゲートするためのものであり、限られた探索手順の中で最良の道を見つけることを目指しています。この図では、特に重要なステップに集中し、バックトラックが少ない最良優先探索のアプローチが視覚化されています。図12で示されたモンテカルロ木探索(MCTS)と比較して、A*探索では全体的に構造がシンプルで、鍵となるステップ周辺での集中度が高いです。これは、効率的な計算と、より洗練された探索手順を取り入れた結果と言えます。