- 小型LLMの数学的思考を向上させるためのrStar-Mathフレームワークの提案
- モンテカルロ木探索を使って最良の解を選びモデルを強化する自己進化型深層思考の導入
- rStar-Mathが計算コストを抑えつつ高い性能を発揮した実験結果
論文:rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking
本記事で使用している画像は論文中の図表、またはそれを参考に作成した画像を使用しております。
本論文の概要
論文「rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking」では、小型のLLMを数学的思考のタスクに適用し、その性能を高める方法が提案されています。この研究は、一般的なLLMの制限を補いつつ、その計算能力を向上させる狙いで行われました。
この研究の中心となる「rStar-Math」フレームワークでは、「自己進化型深層思考」(Self-Evolved Deep Thinking)という手法を導入しました。この手法は、モンテカルロ木探索(MCTS)を活用して問題解決の最良の候補解を選択し、段階的に改善されたデータを生成するプロセスを実現します。初期状態では、LLMは比較的簡単な数学問題を扱うことで開始し、その結果を繰り返し洗練し、難解な課題にも対応可能なモデルを最終的に作り上げます。
具体的には、rStar-Mathは、①ポリシーモデル(解生成用のモデル)と、②リワードモデル(生成結果を評価するモデル)の2つの構成要素を採用します。MCTSを使用して入力された問題に段階的な思考プロセスを適用し、それによって得られる解が正確であるかを評価します。その後、評価の高い解を基にしたデータセットを追加生成し、これを用いてモデルを再訓練する一連の手順を繰り返します。このアプローチは、モデルが解釈力・推論力を徐々に高める手法となっており、「自律的な訓練データ生成」という特長を有しています。
実験では、rStar-MathがMATHデータセットやCollege Mathデータセットなど、複数の数学基準テストで高いパフォーマンスを発揮することが確認されました。特に、推論ステップを伴うコード生成型技術の統合により、他のベースライン手法を上回る成果が得られた点が注目されます。また、この手法では、大規模なLLMと比較しても、計算コストを抑えながら同等の効果を達成できることが示されています。
図表の解説
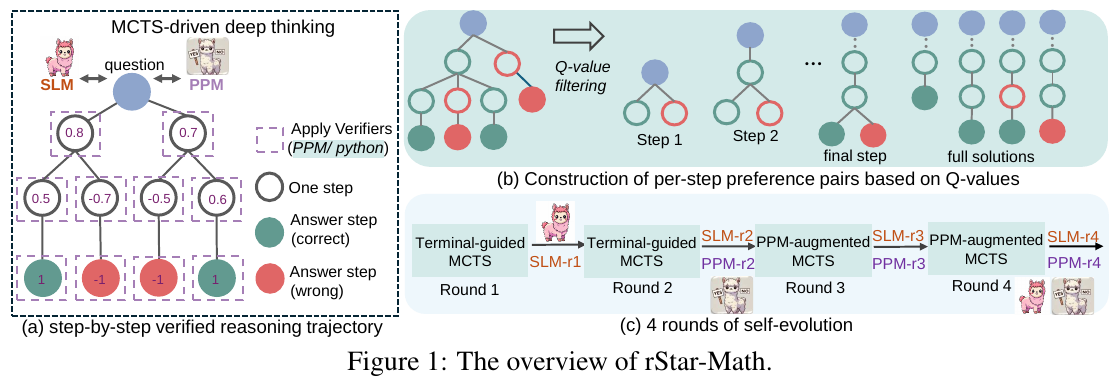
図1はrStar-Mathの概要を示しています。これは小規模な言語モデル(SLM)が数学的な推論能力を向上させるためのフレームワークです。モンテカルロツリー探索(MCTS)を用いて、問題を一歩ずつ確認する推論を行い、正しい推論を構築します。 図の(a)では、MCTSを通じて問題を一歩ずつ解決する過程が示されています。正しいステップは緑、誤ったステップは赤で示され、SLMとプロセス好みモデル(PPM)を用いて検証されます。 図の(b)では、Q値に基づいて各ステップの好みのペアを構築する方法が示されています。これにより、各ステップの正しい推論が選択されます。 図の(c)では、自己進化を通じて4回のラウンドを行い、SLMとPPMが強化され、より高度な数学問題に対応できるよう改善されていく過程を示しています。これにより、SLMが高品質な推論データを自動で生成できるようになります。

表1は、「rStar-Math」が数学推論能力で最先端の性能を発揮することを示しています。この表は、さまざまな数学ベンチマークにおける「rStar-Math」と他のモデルのパフォーマンスを比較しています。「rStar-Math」は、小さな言語モデル(SLM)を使用して独自の進化を遂げ、ベンチマーク問題を解決する能力を高めています。特に、MATHベンチマークでは90.0%の高精度を達成し、他の大規模モデルと同等以上のパフォーマンスを示しています。この結果は、小規模モデルが工夫次第で高度な推論を可能にすることを示唆しています。
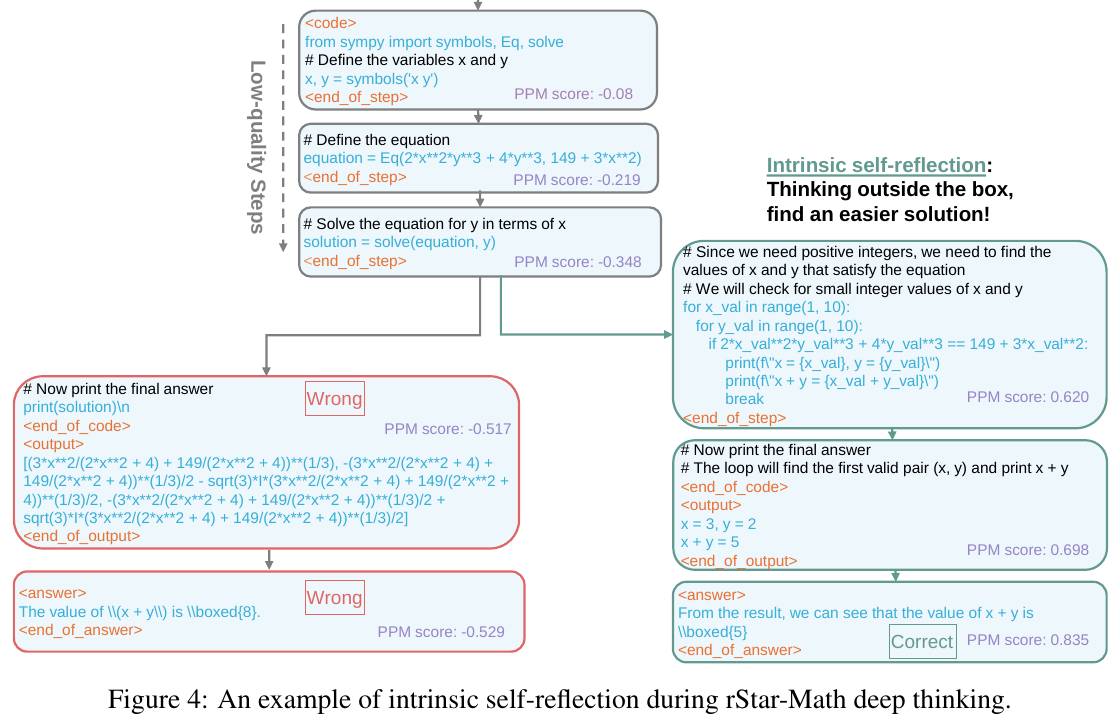
この図は、rStar-Mathの自己内省的な思考プロセスを示しています。まず、モデルは方程式を構築し、SymPyを使って計算しようとしましたが、結果は間違っていました。ここでPPMスコアが低いため、自己内省を行い、より簡単な方法を探すことへと進みました。 次に、モデルはプログラムを修正し、整数範囲内で可能な値を試すループを実装しました。結果として正しい値 \(x = 3, y = 2\) を見つけ、これにより正しい答え \(x + y = 5\) を得ることができました。このプロセスは、PPMスコアの変動によって示されるように、よりよい解決策を見つけるための「内なる反省」および「深い思考」の例とされています。

この画像は、計算問題を解く際に自然言語の説明とPythonコードを組み合わせた「コード強化された連鎖思考 (CoT)」の例を示しています。具体的には、問題をステップごとに分解し、Pythonでそれを計算する過程が示されています。 問題は、特定の距離を歩いた後の初点からの直線距離を求めるもので、ここでは単純な数学の計算がPythonコードで実施されます。各ステップはコメントとして記載され、コードの実行により結果が正確であることが確認されます。 この方法は、CoTの手法により視覚的にステップを追跡し、正確な解答を得るための手段として効果的であることを示唆しています。これは、コードと自然言語の統合が数学的推論の向上に寄与する方法の一例です。
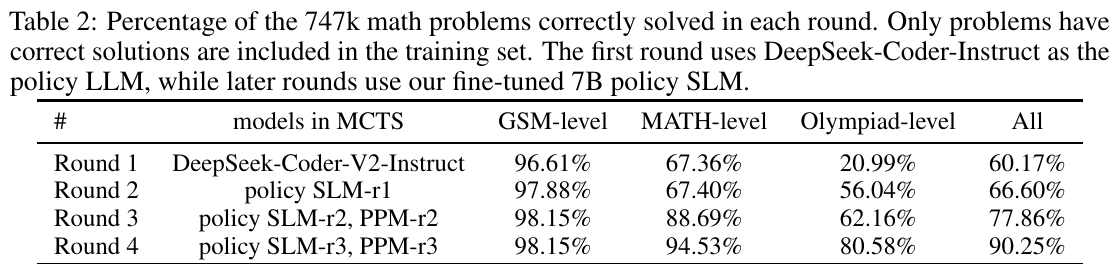
この画像は、論文における4つのラウンドを通じて、747kの数学問題を正確に解決した割合を表しています。初回はDeepSeek-Coder-Instructを使用し、その後のラウンドではファインチューニングされた7BポリシーSLMを使っています。表によると、GSMレベルの問題は最初のラウンドから高い解決率を保っており、MATHレベルはラウンドが進むごとに改善されています。特にオリンピアードレベルの問題は、Round 4で大幅な向上が見られます。総じて、ラウンドを進めるごとに全体の解決率が向上していることが示されています。この表は、モデルの自己進化プロセスが数学的推論能力を向上させていることを示しています。
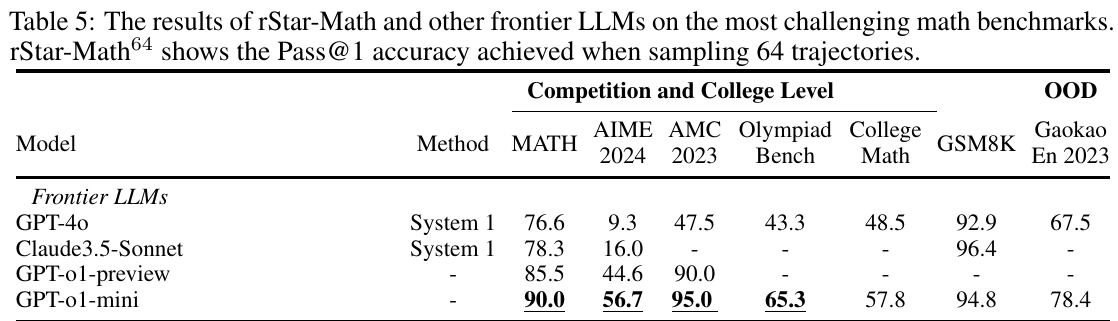
この表は、rStar-Mathと他の最先端のLLMモデルが数学の難しいベンチマークでどの程度の成績を収めたかを示しています。特に、モデルが64の試行を行った際のPass@1の正確さを比較しています。表によれば、rStar-Mathは、さまざまな競技レベルや大学レベルの数学テスト(MATH、AIME 2024、AMC 2023など)において、高い正確さを示しています。特に、GPT-o1-miniモデルが優れた成績を収めており、いくつかの領域では95.0という特に高い精度を示しています。また、rStar-Mathは、GSM8KやGaokao En 2023といったOOD(Out-of-Domain)ベンチマークでも良好な結果を示しています。これは、小規模なモデルが自己進化的な深い思考プロセスを通じて、数理推論の能力を大幅に向上させたことを示しています。
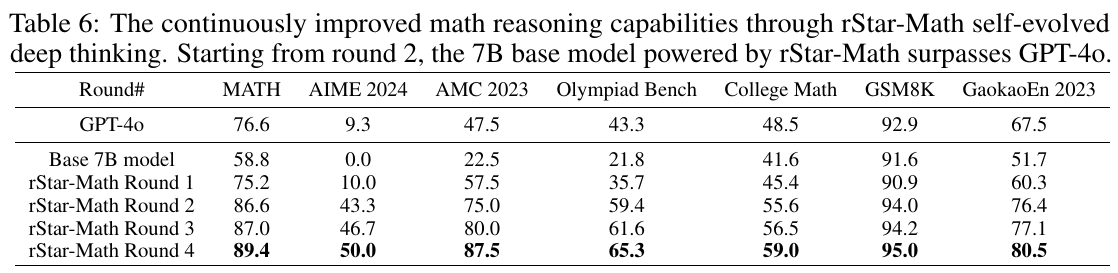
この表は、rStar-Mathという小さな言語モデル(SLM)が数学の推論能力を自己進化的な方法で向上させていく過程を示しています。この方法では、ベースとなる7Bモデルが4回の進化ラウンドを経て、GPT-4oを超える性能を達成しています。具体的には、AIME、AMC、オリンピアッドベンチなどの様々な数学ベンチマークにおいて進化していくにつれて、正解率が向上しています。たとえば、最新のラウンドでは、MATHで89.4%、GaokaoEn 2023で80.5%の精度を記録し、これらのベンチマークでGPT-4oよりも優れています。この表から、rStar-Mathの自己進化的アプローチが小さなモデルであっても数学的推論能力を大幅に向上させることができることがわかります。

画像は、報酬モデルのアブレーション研究に関する表を示しています。PQRM(Process Quality Reward Model)とPPM(Process Preference Model)が、ORM(Outcome Reward Model)よりも数学的推論能力を向上させることを示しています。特にPPMは、数学的推論の最前線を押し進める手法です。表には、さまざまな数学の基準における性能が示されており、PPMを用いた場合に最も高い精度を達成していることがわかります。これは、MCTS(モンテカルロ木探索)を使用したインターフェースプロセスがより有効であることを示しています。つまり、ステップバイステップでの報酬評価がアウトカムベースのモデルよりも優れていることを示唆しています。