- LLMの考えすぎ問題がモデルの効率性と精度に与える影響の分析
- Reasoning Preference Optimizationなどの手法でオーバーシンキングを緩和
- 提案手法が数学テストで精度と効率性を約10%-20%向上
論文:Do NOT Think That Much for 2+3=? On the Overthinking of o1-Like LLMs
本記事で使用している画像は論文中の図表、またはそれを参考に作成した画像を使用しております。
本論文の概要
この論文では、OpenAIのようなモデルをベースとしたo1ライクモデル(例えば、「2+3」のようなシンプルな質問に過剰に思考するモデル)が直面する「オーバーシンキング(Overthinking)」の問題に焦点を当てています。この問題は、簡単な質問にもかかわらず、モデルが複雑で冗長な応答を生成してしまう現象を指します。本研究では、オーバーシンキングがモデルの効率性や回答精度にどのように影響を与えるかを分析し、改善手法を提案しています。
実験では、複数のo1ライクモデル(例えば、QwQ-32B-Preview)を用い、数学的問題や一般知識に基づくテストを実施しました。その結果、モデルは応答生成の初期段階で正解に近い回答を提示することがある一方で、後続のステップで無駄なトークンを生成することが多いと判明しました。これによりプロセス効率が低下し、冗長な回答が生成される傾向が確認されました。
この問題を軽減するため、研究者たちは「Reasoning Preference Optimization(RPO)」や「Simple Preference Optimization(SPO)」といった新しい手法を採用しました。これらは、モデルがより効率的かつ高精度な応答を生成することを促進するもので、学習データの最適化や生成過程の調整を通じてオーバーシンキングを緩和します。また、生成回答の選定アルゴリズムを改善し、一部の冗長なステップを排除することで、計算効率を高めました。
提案手法を評価するため、MATH500やGSM8Kといった数学テストセットで検証を行ったところ、応答精度や効率性が向上したことが示されました。具体的には、正確性を維持しつつ、プロセス効率が約10%から20%改善されました。この結果は、オーバーシンキングの影響を抑えつつ、計算資源の無駄を削減するモデルの可能性を示しています。
図表の解説
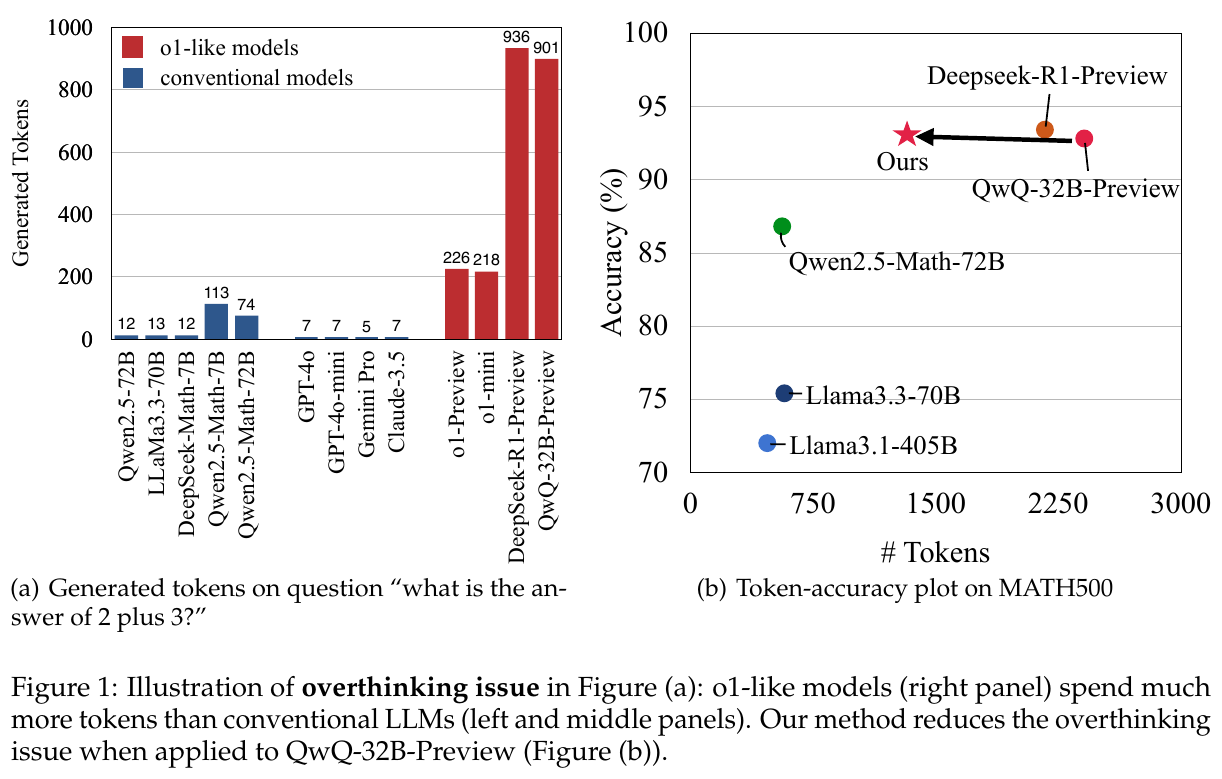
図1の説明:左のグラフ(a)は「2+3の答えは?」という簡単な質問に対して生成されたトークン数を示しています。o1型モデルは、従来のモデルに比べて多くのトークンを生成しています。右のグラフ(b)では、MATH500での精度とトークン数の関連性を示しており、提案手法がQwQ-32B-Previewに適用された際の過剰思考の問題が軽減されたことを示しています。
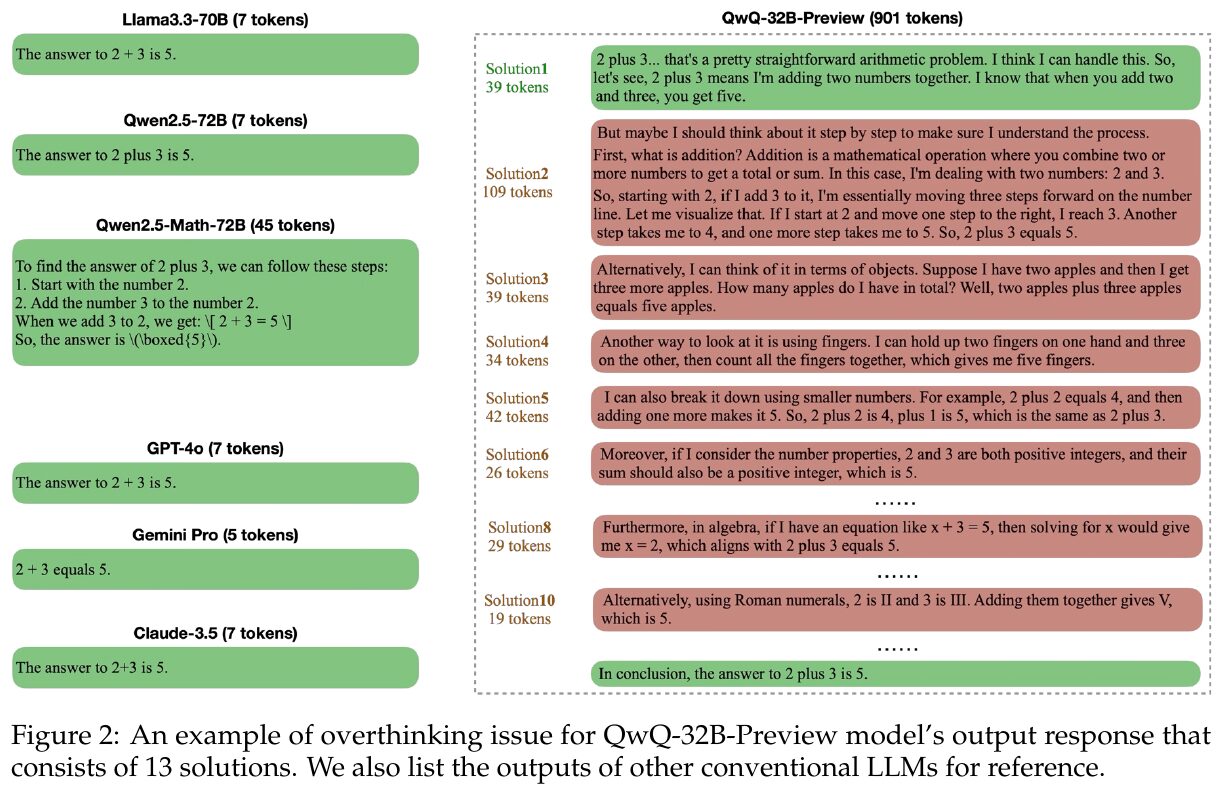
図2は、QwQ-32B-Previewモデルが単純な数学問題「2+3=?」に対し、13もの冗長な解法を生成する例を示しています。他のモデルは単純に「5」と答えるのに比べ、QwQ-32Bは過剰な計算リソースを使用することを示しています。これは「オーバーシンキング」問題の具体例です。モデルが効率的な計算資源を使うことが重要だと強調しています。
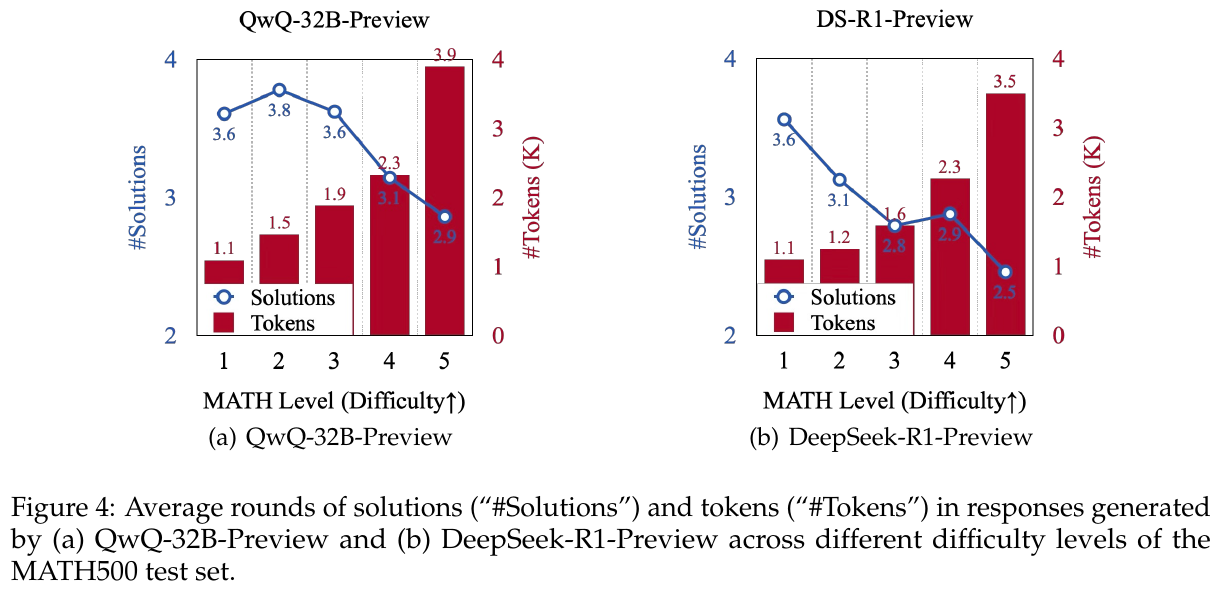
図4は、MATH500テストセットにおけるQwQ-32B-PreviewとDeepSeek-R1-Previewモデルの生成結果を示しています。左のグラフでは、難易度が低い問題ほど多くの解答ラウンドを生成し、トークン数も多くなる傾向があります。右のグラフでは、同様の傾向が見られますが、難易度が高いレベルでも解答数がより少なくなっています。これらは、モデルが簡単な問題に対して過度に考える傾向を示しています。
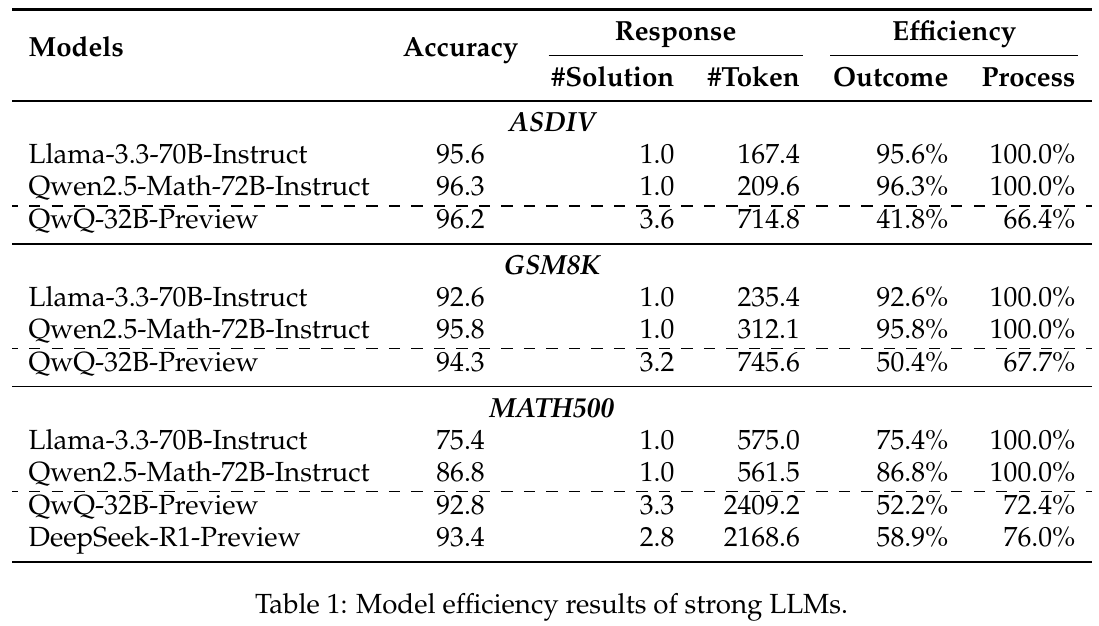
この表は、大規模言語モデル(LLM)の効率性を示しています。ASDIV、GSM8K、MATH500の各データセットにおけるモデルの精度やトークンの使用量、そして効率性を比較しています。特に、QwQ-32B-Previewは他のモデルに比べて多くのトークンを使用する傾向があり、過度な計算をしていることが分かります。この研究は、問題を解決する際の計算資源の効率的な利用について調査しています。
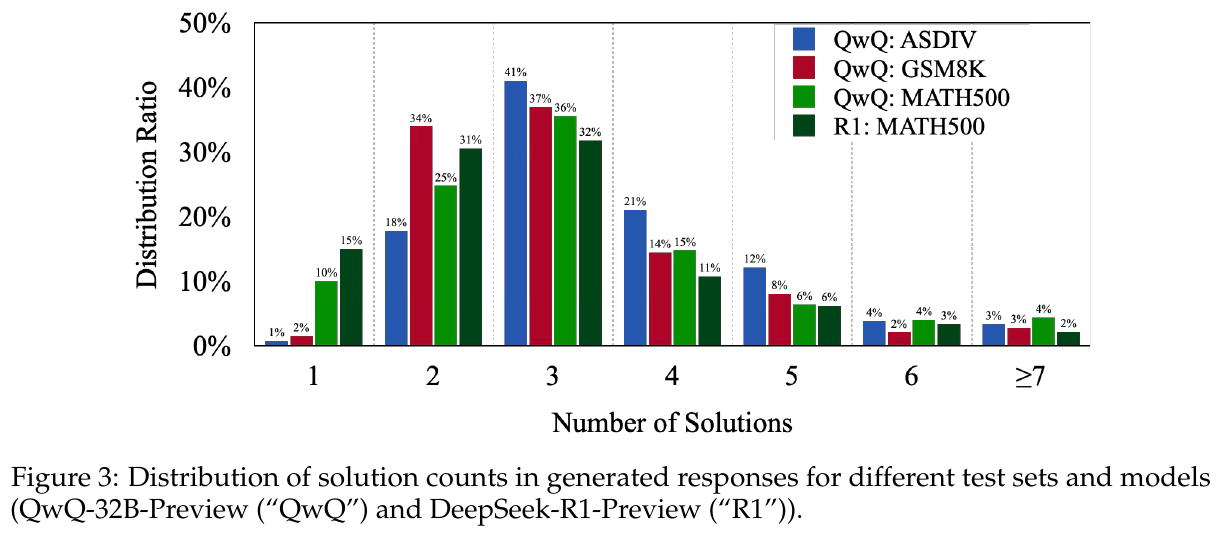
この図は、さまざまなテストセットとモデルの生成された回答における解答数の分布を示しています。QwQ-32B-PreviewやDeepSeek-R1-Previewというモデルが、多くの場合、特定のテストセットにおいて2から4つの解答を生成することがわかります。特に簡単なテストセットでは、多くの解答を生成する傾向があります。
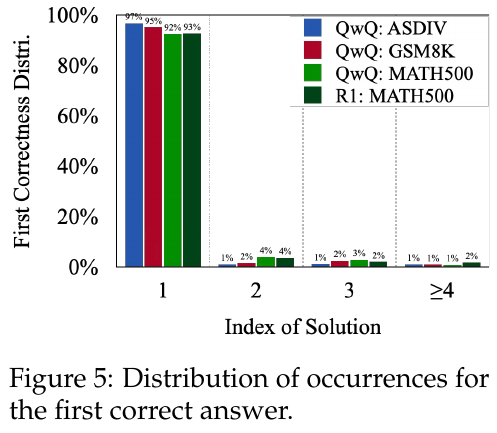
図5は、最初の正解が得られるまでの解答の分布を示しています。QwQモデルとR1モデルを用いたテストセット(ASDIV, GSM8K, MATH500)で、初回の解答が正解を示す割合が非常に高いことが示されています。初回解答で92%以上の確率で正解しており、続く解答は精度向上にほとんど貢献していないことが分かります。これにより、過剰な計算資源の使用が指摘されています。
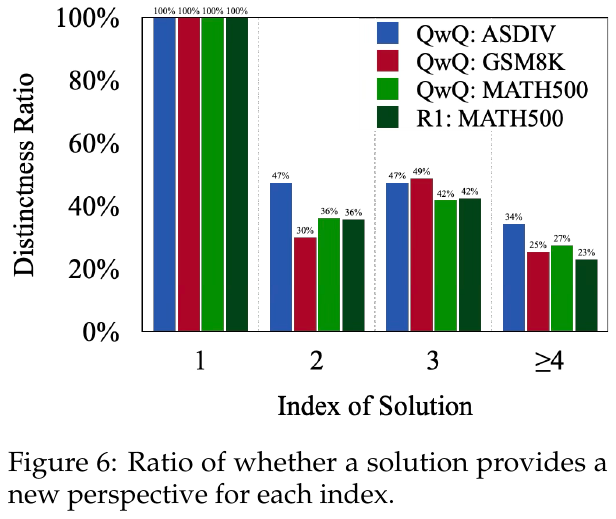
図6は、異なるデータセットで解が新たな視点を与える割合を示しています。図では、ASDIV、GSM8K、MATH500を対象に、1番目の解は常に100%新しい視点を提供していることが示されていますが、解が進むにつれて、異なる視点の割合が減少しています。特に、4番目以降の解では30%以下となり、後続の解は既存のものを繰り返す傾向があります。これは、早期の解決策が新しい視点を提供し、後の解決策は有効性が低いことを示唆しています。
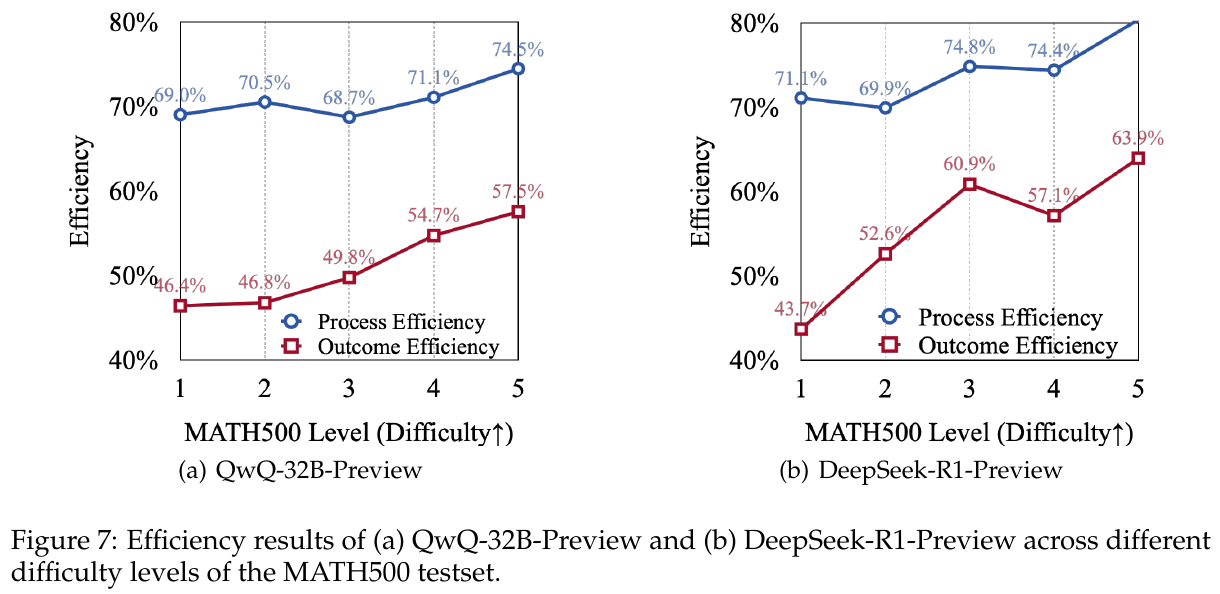
図7は、MATH500テストセットの異なる難易度における「QwQ-32B-Preview」と「DeepSeek-R1-Preview」の効率性を示しています。どちらのモデルも難易度が上がるほどプロセス効率とアウトカム効率が高まる傾向がありますが、簡単な問題では効率が低下しています。これにより、モデルがシンプルな問題で過剰に考える傾向が浮き彫りになっています。